2021-02-26

- 정의
집합론에서, 곱집합(곱集合, 영어: product set , product) 또는 데카르트 곱(Descartes곱, 영어: Cartesian product 카티지 언 프로덕트)은 각 집합의 원소를 각 성분으로 하는 튜플들의 집합이다.

(출처 : 위키백과)
말은 굉장히 거창하고 어려워 보인다. 하지만 위의 이미지를 한 번 보자. A를 구성하는 집합은 (x, y, z) B를 구성하는 집합은 (1, 2, 3)인 것을 확인할 수 있다. 이후 이 둘은 곱하면 이 두 집합 간 구성원들이 만날 수 있는 모든 경우의 수로 새로운 테이블을 만들어지는 것을 확인할 수 있다.
- 예제
이제 SQL 내부에서의 카티션 프로덕트를 알아보자. 우선 곱하기 위해 준비한 두 가지의 테이블을 보자 ( 아래 테이블의 코드가 궁금하면 아래 링크를 확인하자 )
SELECT * FROM CLIENTINFO;

SELECT * FROM CLIENTJOIN;
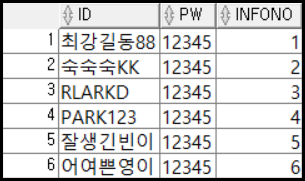
테이블의 내용은 위와 같으며, CLIENTINFO의 기본키는 INFONO이며, CLIENTJOIN 기본키는 ID이며 CLIENTINFO의 INFONO를 쓰고 있다. 이제 이 두 테이블을 카티션 프로덕트를 해보자
- 카티션 프로덕트(Cartesian Product)
사실 코드는 매우 간단하다. 조인조건을 부여하지 않고 아래와 같이 SELECT * 로 전체 테이블을 선택한 후 FROM을 이용해 동시에 두 개의 테이블을 불러오면 된다.
SELECT * FROM CLIENTINFO, CLIENTJOIN;
위의 코드의 결과는 아래와 같으며, 두 테이블 간의 관계에서의 모든 경우의 수를 합쳐 테이블로 출력하게 된다.
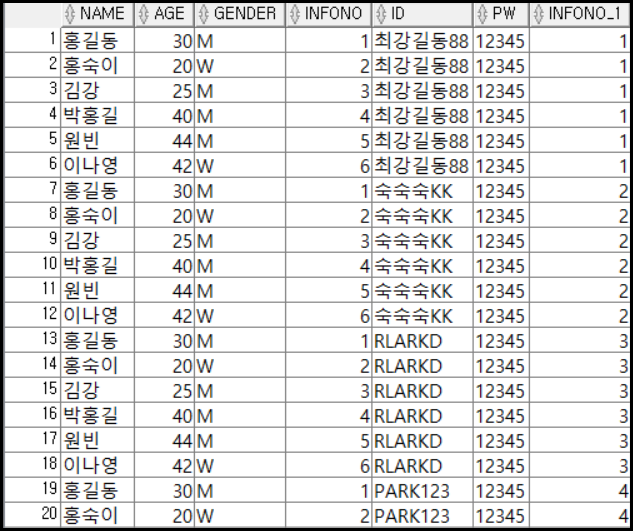

여기서 중요한 점은 카티션 프로덕트 후 튜플(행)의 수는 각 테이블의 곱과 같고, 속성(컬럼)의 수는 각 테이블의 속성들을 더한 것과 같다는 점이다.

